Dirac Delta-function

To visualise the Dirac $\delta$-function, we treat it like a single infinite spike at $t=a$ coming from the limit of a sequence of top-hat functions; let the height of the top-hat be $\frac{1}{\Delta t}$ and width be $\Delta t$, so $\Delta t$ shrinks and $\delta$ concentrates ($\delta (t-a)=0,t\ne a:{\int }_{-\infty }^{\infty }\delta (t-a)dt=1$).

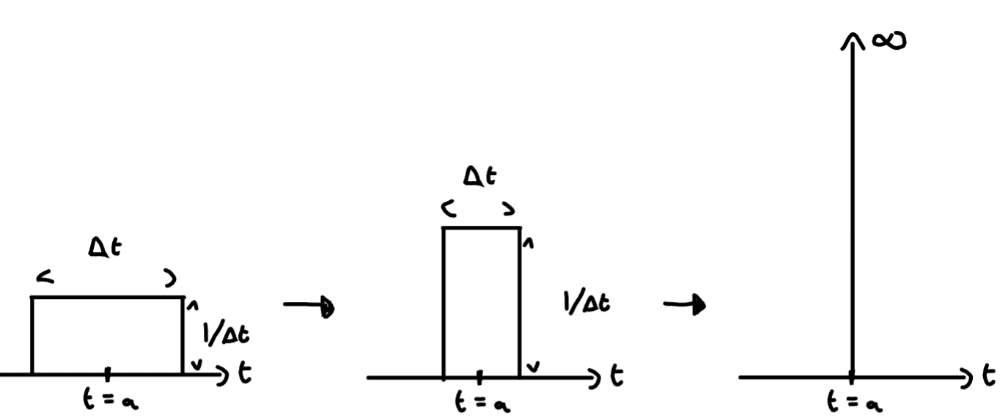
An integral involving the Dirac $\delta$ function essentially calculates the value of an integral at one precise point, as the function is equal to zero apart from where it spikes at $a$; hence just equal to the function value at that point, $f(a)$.

Mathematically, for $[f(t)\times \delta (t-a)]$ all contributions from either side of the spike at $t=a$ are zero, such that the one remaining contribution is:

$$\underset{\Delta t\to 0}{\lim }f(a)\left(\frac{1}{\Delta t}\right)\cdot \Delta t=f(a)$$

So that ${\int }_{-\infty }^{\infty }f(t)\delta (t-a)dt=f(a)$: the sifting property of the $\delta$ function (or simply the definition).

The $\delta$ function copies functions to its location(s) when finding the convolution between it and another function.